Échange
Pourquoi échanger entre consommateurs? Par quel moyen? Par le troc, un marché ou bien en nommant quelqu’un qui se chargera de partager les biens entre les personnes. Quel mécanisme fera le mieux?

Nous verrons qu’il existe généralement des gains à l’échange. L’échange peut seulement être bénéfique. Si ce ne l’est pas, les individus n’échangent pas. Donc permettre l’échange ne peut nuire. Le meilleur résultat peut être atteint de différentes façons (marché, planificateur central, troc) si certaines conditions sont respectées.
Débutons avec un cadre simple, qui ne restreint pas la généralité des résultats plus tard:
Considérons une situation avec deux consommateurs (1 et 2) et deux biens (\(X\) and \(Y\))
Fonctions d’utilité \(U_1(X,Y)\) et \(U_2(X,Y)\)
Chaque consommateur a une dotation de chacun des biens, \(B_1^e = (X_1^e,Y_1^e)\) et \(B_2^e = (X_2^e,Y_2^e)\).
Exemples
Deux fermiers, un a une dotation de pommes de terre et l’autre de bétail.
Deux pays: Le pays 1 a une dotation de pétrole, le pays 2 de la machinerie industrielle.
Deux consommateurs sur kijiji ou Ebay: l’un a un canot et l’autre un ordinateur portable
D’où viennent ces dotations? Pour le moment, de la nature (ressources naturelles ou héritage?). Plus tard, ces dotations proviendront des profits provenant de la production d’un bien à l’aide d’autres biens dans l’économie.
Équilibre de marché
Le marché est une forme d’échange très répandue. En termes de modélisation, le marché est résumé par un vecteur de prix (s’il y a plusieurs biens) et un système légal qui encadre les transactions.
Si chaque consommateur a une dotation et une demande individuelle pour les biens en fonction des prix, on peut assez facilement trouver un équilibre de marché, ici d’échange, puisqu’il n’y a pas de production. Pensez à Kijiji.
En premier lieu, on trouve les demandes des consommateurs.
Le Consommateur \(i=1,2\) choisi de consommer \((X_i^c, Y_i^c)\) en maximisant son utilité.
Étant donné les prix \(p_X\) and \(p_Y\), la contrainte budgétaire de chacun des agents est
\[p_X X_i^c + p_Y Y_i^c = p_X X_i^e + p_Y Y_i^e\]
Ceci donne les demandes marhalliennes: \((X^c_i(p_X,p_Y), Y^c_i(p_X,p_Y))\).
En deuxième lieu, les prix sont déterminés en équilibre. Pour cette deuxième étape, on doit d’abord faire une observation.
Réalisons d’abord que ce n’est que le prix relatif qui est important pour l’équilibre. Nous avons deux prix inconnus \(p_X\) et \(p_Y\). La contrainte budgétaire peut être ré-écrite
\[X_i^c + \frac{p_Y}{p_X} Y_i^c = X_i^e + \frac{p_Y}{p_X} Y_i^e, \quad i=1,2\]
On peut donc, sans perdre d’information, dénoter \(p = p_Y/p_X\), le prix relatif de \(Y\) en terme de quantité de \(X\) . On aurait aussi pu définir le prix comme étant \(p = p_X/p_Y\)!
Comment trouver le prix relatif d’équilibre?
Étape 1: Demande individuelle: On cherche
On obtient \(X_i^c(p)\) et \(Y_i^c(p)\) par le lagrangien.
Étape 2: Le prix \(p^*\) est un prix d’équilibre si à \(p^*\) la demande agrégée est égale à l’offre agrégée. On cherche donc \(p^*\) tel que:
\[X_1^c(p^*)+X_2^c(p^*) = X_1^e + X_2^e \quad et \quad Y_1^c(p^*)+Y_2^c(p^*) = Y_1^e + Y_2^e\]
La quantité de \(X\) échangée est donnée par \(X_1^c(p^*) - X_1^e =X_2^e - X_2^c(p^*)\). Si \(X_1^c - X_1^e < 0\), le consommateur 1 est offreur de \(X\) (le consommateur 2 demandeur).
Important
Hypothèses importantes:
Le marché est compétitif: Le consommateur prend le prix comme donné. Il est preneur de prix.
Tous les biens sont homogènes (identiques) et perçus de la même façon par l’acheteur et le vendeur.
L’utilité du consommateur 1 ne dépend pas des actions des autres consommateurs: aucune externalité
À faire
Exercice A: Trouvez le prix d’équilibre pour un marché avec \(u_1(X,Y) = u_2(X,Y) = \log X + \alpha \log Y\). Fixez \(p_X= 1\), et donc \(p_Y = p\). Les dotations sont données par \((X_1^e, Y_1^e, X_2^e, Y_2^e)\).
Loi de Walras
On a deux choix de marché pour trouver le prix d’équilibre. Donc, une seule inconnue \(p\) mais deux équations… L’équilibre sur un marché implique l’équilibre sur l’autre. Regardons les deux contraintes budgétaires:
\[X_1^c + p Y_1^c = X_1^e + p Y_1^e \quad et \quad X_2^c + p Y_2^c = X_2^e + p Y_2^e\]
Si on additionne les deux contraintes, on obtient:
\[[X_1^c + X_2^c] + p [Y_1^c + Y_2^c] = [X_1^e + X_2^e] + p[Y_1^e + Y_2^e]\]
Un équilibre pour \(X\) implique que
\[p[Y_1^c + Y_2^c] = p [Y_1^e + Y_2^e] \Rightarrow Y_1^c + Y_2^c = Y_1^e + Y_2^e\]
Important
La loi de Walras permet de se concentrer sur le prix relatif et de trouver le prix d’équilibre sur un seul des marchés sans avoir à regarder l’autre. On peut généraliser cette loi à plus de 2 biens.
Est-ce que l’équilibre de marché garantit le niveau de bien-être le plus élevé que peuvent obtenir les deux agents? Afin de juger de l’allocation de marché, nous devons faire un pas de côté pour définir une allocation optimale, sans le recours au marché.
Allocation Pareto-efficace
On a déjà vu qu’une amélioration de Pareto est possible quand aucun des deux agents ne perd en utilité et qu’au moins un gagne.
Important
Quand il n’existe plus d’amélioration au sens de Pareto, on dit que l’allocation est Pareto optimale ou efficace.
Nous allons maintenant appliquer ce principe aux allocations de biens.
Pour ce faire, on aura besoin d’une boîte d’Edgeworth, un outil très utile. C’est en fait un système de coordonnées qui permet de tracer en deux dimensions un problème qui en a 4 (les quantités des biens \(X\) et \(Y\) pour les consommateurs 1 et 2). Pour ce faire, on utilise le fait qu’il existe une quantité totale fixe des biens X et Y. L’exercice A vous apprendra à construire une boîte d’Edgeworth.
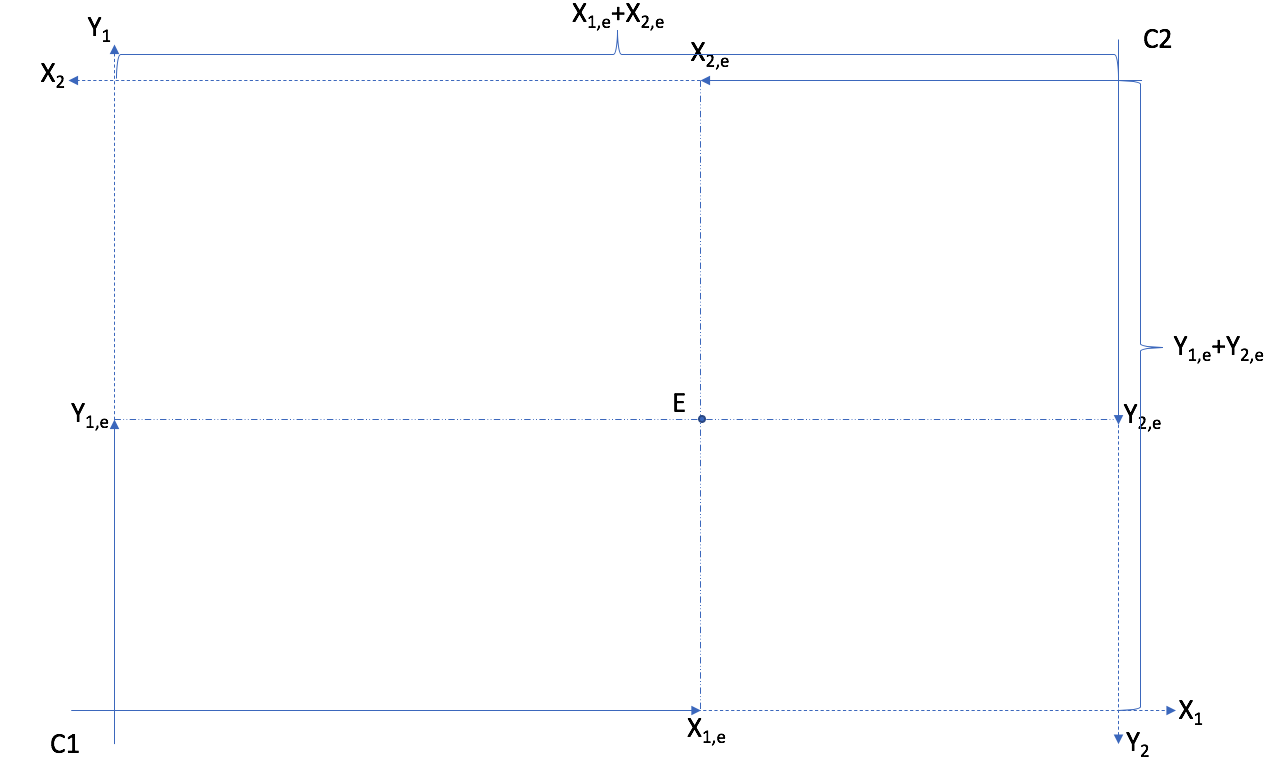
La boîte a des dimensions égales aux dotations totales des biens \(X\) et \(Y\).
À faire
Exercice B: Montrer la \((x^e_1,y_1^e) = (50,20)\) et \((x^e_2,y_2^e)=(20,50)\) dans une boîte d’Edgeworth.
À faire
Comprendre le boîte d’Edgeworth avec un exemple de EconGraph.org
Un certain nombre d’observations peuvent être faite à partir de la boîte d’Edgeworth.
D’abord, un point dans une boite d’Edgeworth où deux courbes d’indifférence se croisent ne peut être Pareto optimal. Pourquoi? Parce qu’on peut définir un noyau par rapport à ce point comme étant toutes les allocations qui mènent à une amélioration de Pareto.
Important
Le noyau d’une allocation représente toutes les autres allocations qui mènent à une amélioration au sens de Pareto.
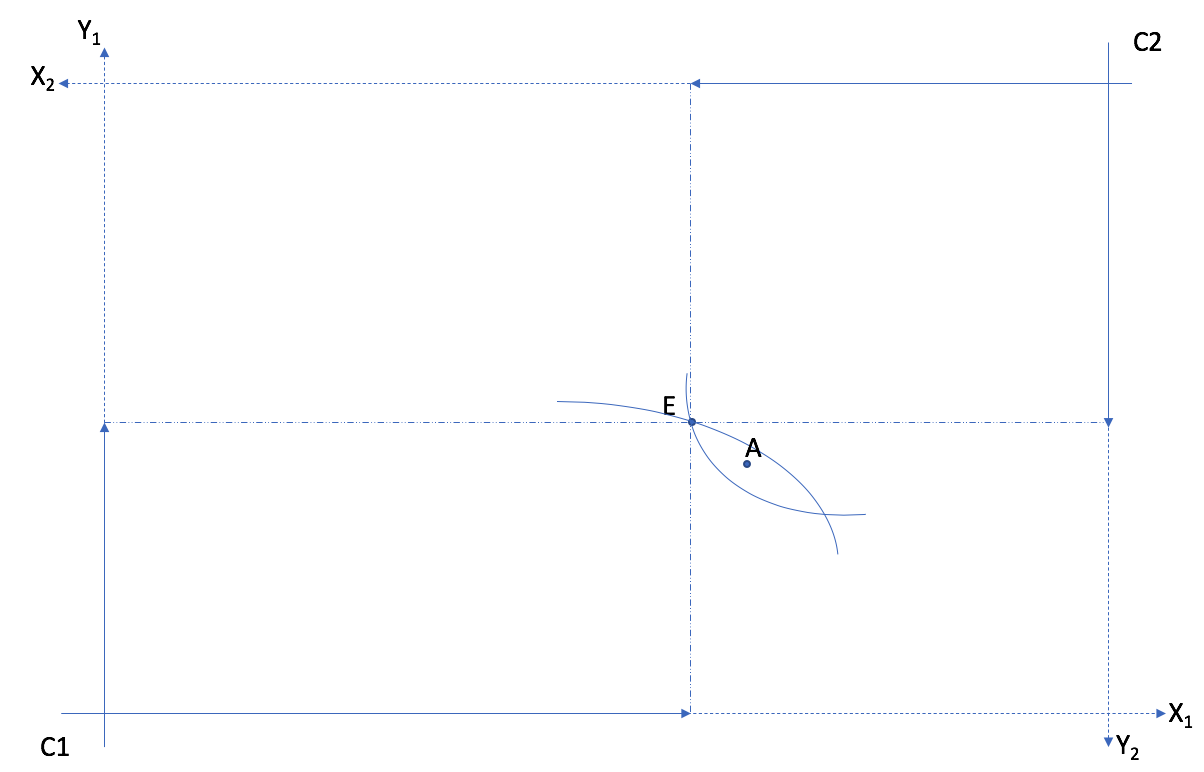
L’allocation E n’est pas optimale: les courbes d’indifférences se croisent. L’allocation A est une amélioration au sens de Pareto. Le noyau est cette zone entre les deux courbes d’indifférences.
Quand le noyau est vide, l’allocation est Pareto efficiente ou optimale. Ceci implique que les courbes d’indifférences doivent être tangentes.
Important
Une allocation est optimale au sens de Pareto si son noyau est vide. Les TMS sont alors égaux.
Important
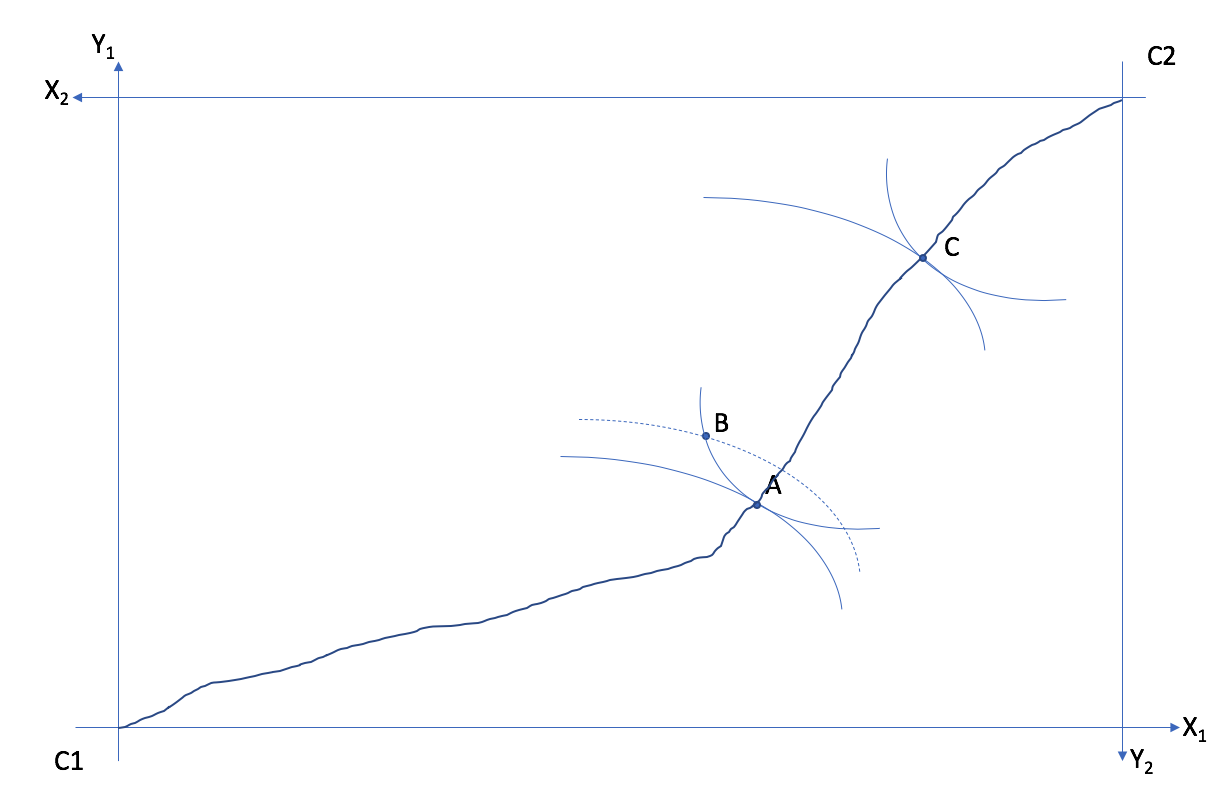
La courbe des contrats est la courbe qui passe par toutes les allocations Pareto optimale.
La frontière de Pareto est la courbe dans l’espace \((U_1,U_2)\) qui indique toutes les allocations optimales au sens de Pareto.
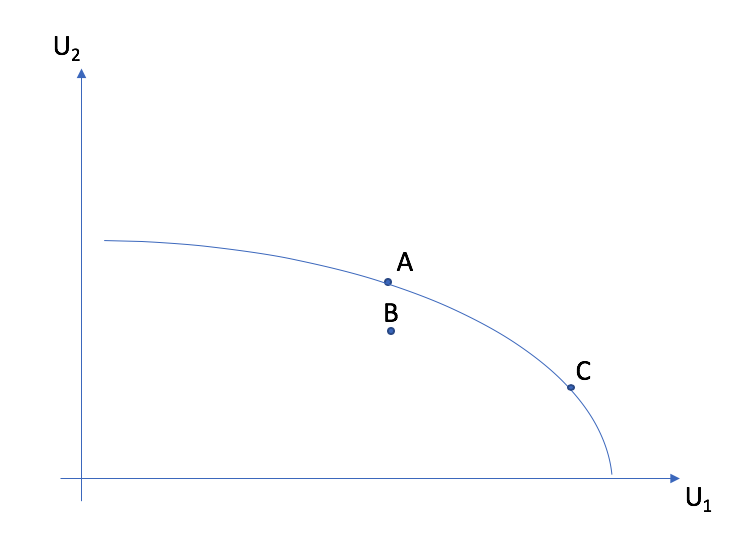
Les allocations A et C sont optimales au sens de Pareto. Elles se retrouvent sur la courbe des contrats et sur la frontière de Pareto. Cependant, l’allocation B n’est pas optimale: les courbes d’indifférence se croisent et elle est à l’intérieur de la frontière de Pareto.
Comment calculer un optimum de Pareto? On peut utiliser le principe de la maximisation contrainte. On pourrait tenter de maximiser le bien-être d’un agent, tout en gardant le bien-être d’un autre agent fixe et en respectant la contrainte de ressources. Ceci se fait à partir d’une dotation initiale. Si la solution à ce problème est la dotation initiale, alors la dotation est Pareto optimale. Sinon, la solution nous donne une allocation dans le noyau par rapport à ces dotations initiales.
On applique la technique du lagrangien, mais cette fois avec trois contraintes. Voici le lagrangien:
où \(X_e = X^e_1 + X^e_2\) et similairement pour l’autre bien.
Il y aura donc 6 CPO et 3 multiplicateurs. De ces CPO on va dériver la condition suivante pour trouver les allocations Pareto optimales,
Important
Dans toute allocation optimale au sens de Pareto, les TMS sont égaux.
Les exercices qui suivent vous aideront à comprendre la démarche pour la solution.
À faire
Exercice C: Trouvez l’allocation Pareto optimale pour les fonctions d’utilité \(u_1\) et \(u_2\) strictement positive and concave, \(u_j = \sqrt{x_j y_j}\) pour les consommateurs \(j=1,2\), en utilisant la méthode du Lagrangien.
À faire
Exercice D: Trouvez l’allocation Pareto optimale pour les fonctions d’utilités \(u_j = \sqrt{x_j y_j}\) pour les consommateurs \(j=1,2\) avec les dotations \(x_e = 128\) et \(y_e=32\) si \(\overline{u}_2=48\).
À faire
Exercice E: Dans l’exercice D, l’allocation \((64,28,64,4)\) est-elle optimale au sens de Pareto? Si elle ne l’est pas, trouvez une amélioration au sens de Pareto dans le noyau.
Équilibre de marché dans une boîte d’Edgeworth
La contrainte budgétaire dépend des dotations et indique les allocations qui sont possibles au prix \(p\). Un équilibre de marché implique que le \(TMS\) est égal au prix. Puisque le prix est le même pour les deux consommateurs, les \(TMS\) sont égaux dans un équilibre de marché.
Important
Dans un équilibre de marché, les TMS des consommateurs sont égaux au même prix relatif et donc sont égaux.

Un équilibre de marché est donné par A. Il est réalisé à partir de dotations représentées au point E. Le prix relatif \(p = p_Y/p_X\) donc une droite avec pente \(-p_X/p_Y = -1/p\).
À faire
Un exemple d’équilibre de marché dans le boite d’Edgeworth de EconGraph.org.
Échange, Marché et bien-être
Considérons le prix d’équilibre: \(p^*\) et les quantités consommées par le consommateur 1: \(X^c_1 = X^c_1(p^*)\) et \(Y^c_1 = Y^c_1(p^*)\). On a que \(u_1(X^c_1, Y^c_1) \geq u_1(X^e_1, Y^e_1)\)
Pourquoi? Au prix \(p^*\), le panier de dotations \(B^e_1 = (X^e_1,Y^e_1)\) est disponible, mais le consommateur préfère \(B^c_1=(X^c_1, Y^c_1)\). Donc, les choix révèlent que \(u_1(X^c_1, Y^c_1) \geq u_1(X^e_1, Y^e_1)\).
Donc, le consommateur ne peut que gagner si l’échange survient dans le marché.
Théorème du bien-être
Important
Premier théorème du bien-être: Un équilibre de marché est toujours optimal au sens de Pareto.
Si une allocation est Pareto-optimale, on ne peut améliorer le sort d’un consommateur sans réduire celui d’un autre.
Pourquoi ce résultat? À l’allocation d’équilibre \((X^c_1(p^*),Y^c_1(p^*),X^c_2(p^*),Y^c_1(p^*))\) les courbes d’indifférences sont tangentes à la même contrainte budgétaire (le rapport de prix égal au TMS pour les deux, mais il s’agit du même prix!). Si elles sont tangentes, c’est donc qu’on a une allocation Pareto optimale.
À faire
Jouez avec ce exemple: EconGraph.org.
Important
Deuxième théorème du bien-être: On peut obtenir n’importe quelle allocation Pareto optimale par un équilibre de marché où on devra redistribuer les dotations.
Ceci nécessite la possibilité d’imposer des taxes, ou redistribuer des dotations: paiements ou taxes dites lump-sum. On dit alors que l’allocation des ressources est décentralisée (le fruit d’un équilibre de marché et de redistribution des dotations).
Pourquoi ça fonctionne?
Pour toute allocation \((X_1^*,Y_1^*)\), et valeurs conséquentes pour \((X_2^*,Y_2^*)\), les courbes d’indifférence sont tangentes. À cette ligne de tangence, on peut redistribuer les dotations pour trouver un point sur cette ligne. N’importe quelle dotation finale (après transfert) sur cette ligne, mène à un équilibre de marché avec \((X^*,Y^*)\).
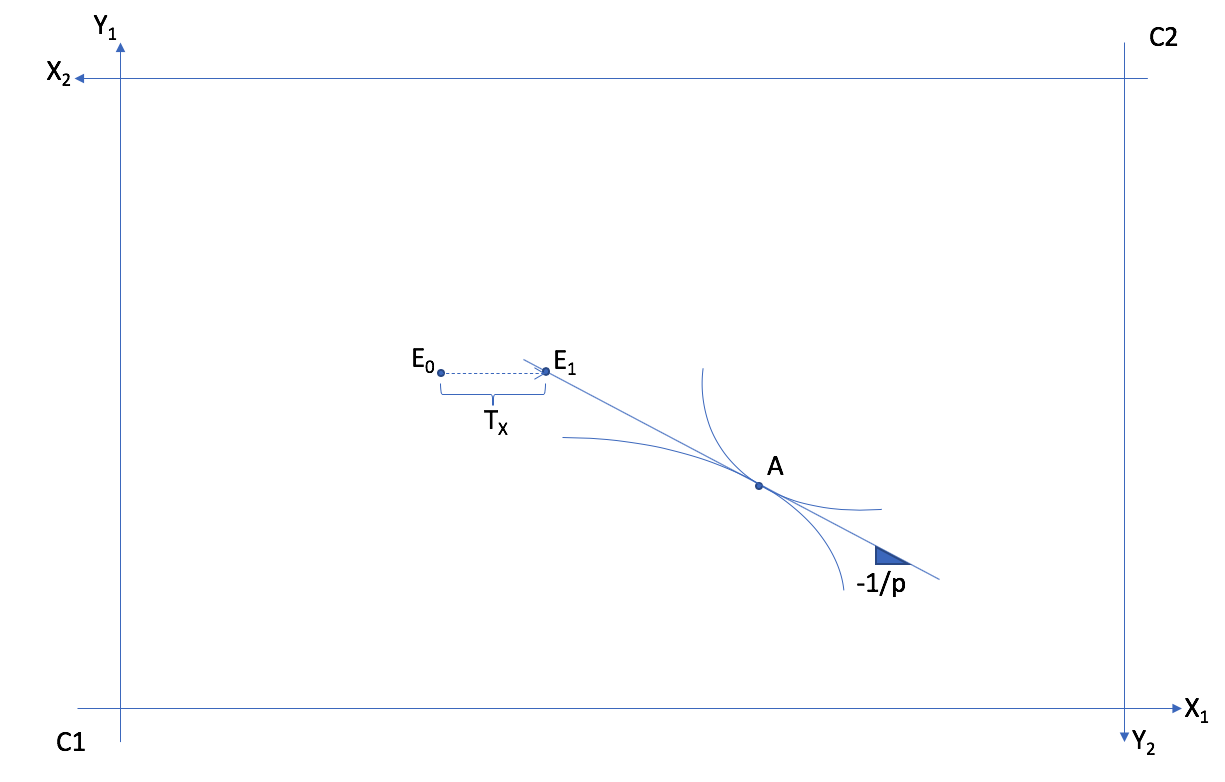
L’optimum de Pareto A n’est pas atteignable à partir de la dotation \(E_0\). Mais un transfert de \(T_X\) du bien \(X\) provenant du consommateur 2 au consommateur 1, permet d’atteindre la dotation \(E_1\), à partir de laquelle on peut attendre l’optimum de Pareto A avec un équilibre de marché au prix \(p\).
À faire
Exercice F: Trouvez le transfert de dotation et le prix, partant de \((64,28,64,4)\), qui donne l’allocation trouvée à l’exercice E.
À faire
Jouez avec cet exemple de EconGraph.org.
Efficience des marchés
Les premier et deuxième théorèmes établissent que
Le marché est efficient, il mène à un optimum de Pareto
Si on veut une autre allocation optimale, on peut l’obtenir est redistribuant les ressources et en laissant le marché faire son travail.
C’est un résultat important en économie, car il permet d’atteindre l’optimum de Pareto tout en ne restraignant pas la liberté de choix des consommateurs.
Important
L’économie de marché permet d’obtenir ce que le planificateur aurait pu faire sans sacrifier la liberté des agents économiques.
Un équilibre de marché nécessite seulement que les agents connaissent leur propre préférences. Il n’y a pas de besoin pour un planificateur central qui connait les préférences de tous. Selon Hayek, les marchés sont des agrégateurs d’information. Les économies planifiées perdent cette information (sans mentionner le coût énorme de réussir à connaître les préférences de tous les citoyens).
Limitations
Important
Ces résultats encourageants reposent cependant sur des hypothèses très fortes: - Marchés sont compétitifs (on a des preneurs de prix) - Les biens sont homogènes (on sait ce qu’on achète) - Aucune externalité - On peut imposer des taxes forfaitaires (pour le 2e théorème)
Même si son cadre est simpliste, et certains diront que peu de marchés remplissent ces conditions, il s’agit d’un modèle qui permet de fixer un benchmark, ou un contre-factuel, afin de réfléchir aux failles de marchés de manière précis et structuré.
La théorie de l’équilibre générale a eu un impact certain sur l’économie: en particulier en macroéconomie et pour les marchés financiers. Les gouvernements, mais aussi d’autres organisations utilisent ces modèles pour prédire l’effet de différentes politiques, notamment en ce qui attrait au climat.
Un peu d’histoire

Kennet Arrow et Gérard Debreu sont ceux qu’on créditent habituellement pour avoir montré l’existence de l’équilibre général. Ils venaient de background très différent et étaient intéressés à cette question pour des raisons différentes. Düppe (2017) raconte et documente comment ce projet s’est réalisé, non sans des tensions évidentes.

Voir cette entrevue avec Till Duppe, Professeur titulaire à l’ESG UQAM, grand spécialiste de l’histoire de la pensée économique.
Exemple Python
Dans ce notebook, nous explorons comment trouver la solution d’un problème d’échange ainsi que le prix d’équilibre.