Le Temps
Préférences
Les individus préfèrent généralement un bénéfice le plus tôt possible et un coût le plus tard possible:
Un café maintenant ou dans une heure?
Aller au Gym aujourd’hui ou demain?
Épargner aujourd’hui pour dépenser demain?
L’évidence empirique indique que l’origine de ces préférences peut-être tracée à l’enfance…
Utilité escomptée
Dans son livre The Theory of Interest en 1930, Irving Fisher présente une théorie assez simple, mais qui servira de modèle pour des centaines de travaux en micro et macroéconomie. Les préférences y sont représentées par l’utilité escomptée.
Si \(u(C_t)\) est l’utilité de consommer à la période \(t\), l’utilité escomptée pour un plan de consommation \(\textbf{C} = (C_1,...,C_T)\) est :
\(\delta\) \(\in [0,1]\) est le facteur d’escompte (patience) alors que \(\mathbf{C} = (C_1,...,C_T)\). La relation entre le facteur d’escompte et le taux d’escompte \(\rho\) est donné par:
Taux marginal de substitution (TMS)
Si \(T=2\), alors
La différentielle totale donne le TMS:
Important
Les préférences intertemporelles sont caractérisées par le facteur d’escompte (\(\delta\)) et la forme de \(u\).
À faire
Exercice A: Trouvez le TMS pour \(u(C_t) = \log C_t\)
Comment estimer le taux d’escompte? On peut utiliser les listes de prix multiples.
Une expérience au Danemark réalisée auprès de fonctionnaires Danois a permis d’estimer le facteur d’escompte au niveau individuel (Harrison, Lau and Williams, 2002)
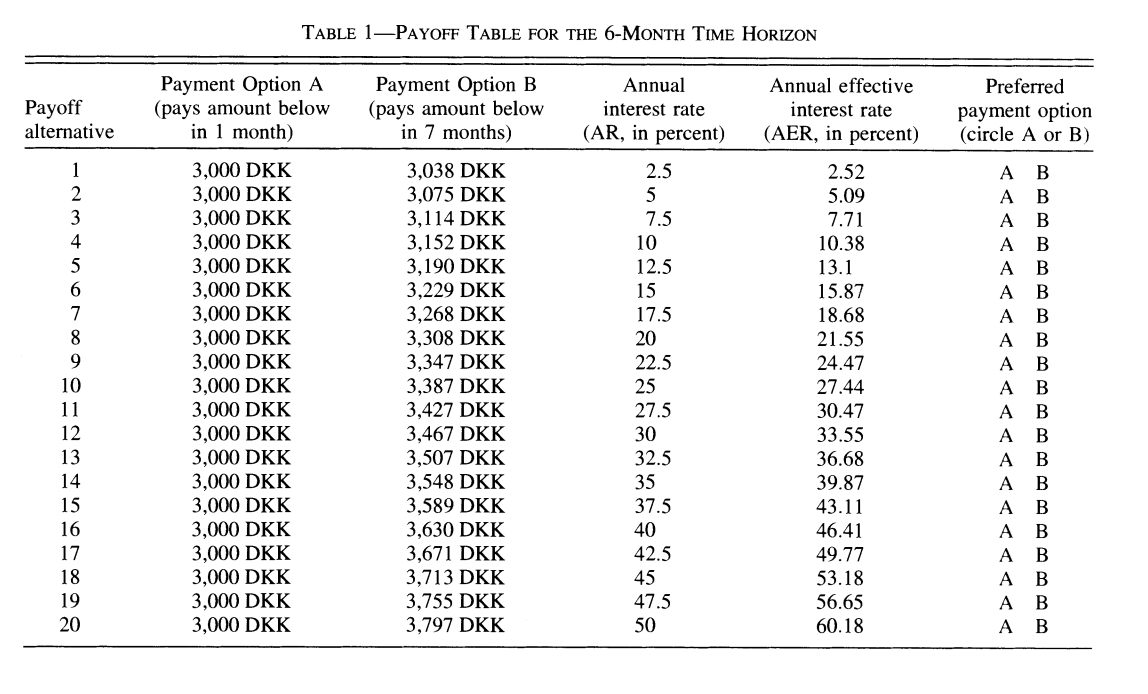
Les résultats montrent une grande dispersion et des taux d’escompte élevés, beaucoup plus élevés que les taux d’intérêts.
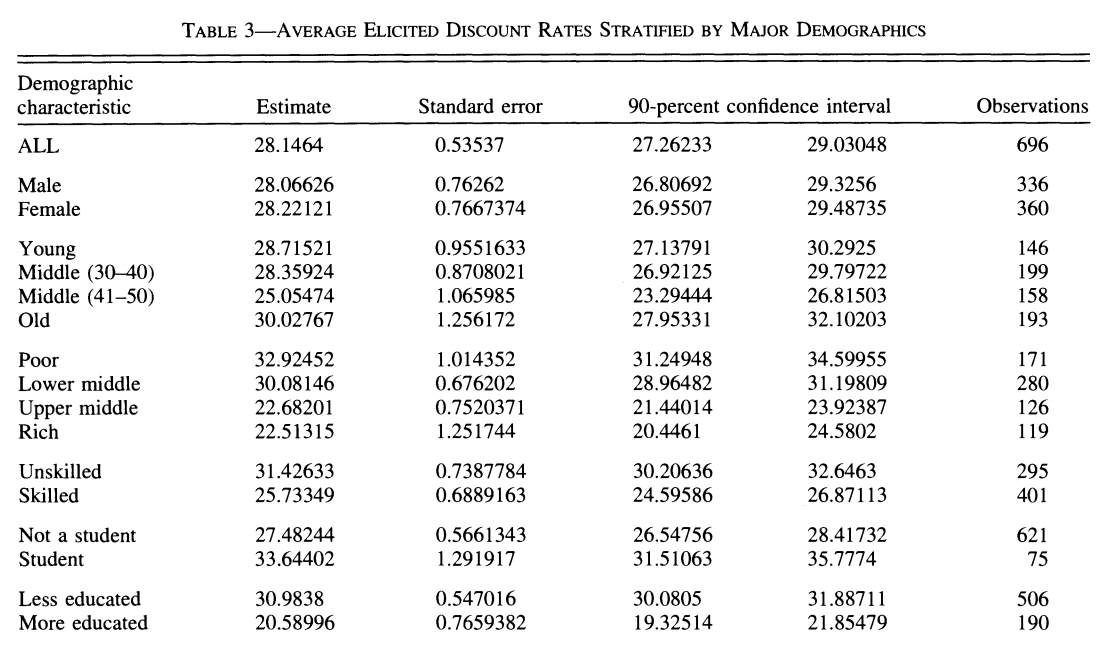
La contrainte intertemporelle
Marché financier et intérêt
Institution financière offre \(r_S\) pour chaque dollar déposé (épargne). Elle nous demande \(r_D\) pour chaque dollar prêté
Supposons pour le moment \(r_D = r_S = r\).
Ressources
Les ressources proviennent de:
Richesse initiale: \(W_0\).
Revenu dans les deux périodes, \(Y_1\), \(Y_2\).
La valeur présente des ressources est :
Constrainte
La valeur présente de la consommation est:
Ainsi, la contrainte intertemporelle est \(VP_C \leq VP_W\):
Emprunt et épargne
On peut écrire la contrainte comme étant :
Important
L’individu qui épargne en première période, peut consommer plus que son revenu en 2e période. L’individu qui emprunte en première période, doit consommer moins que son revenu en 2e période.
Visuellement, on a
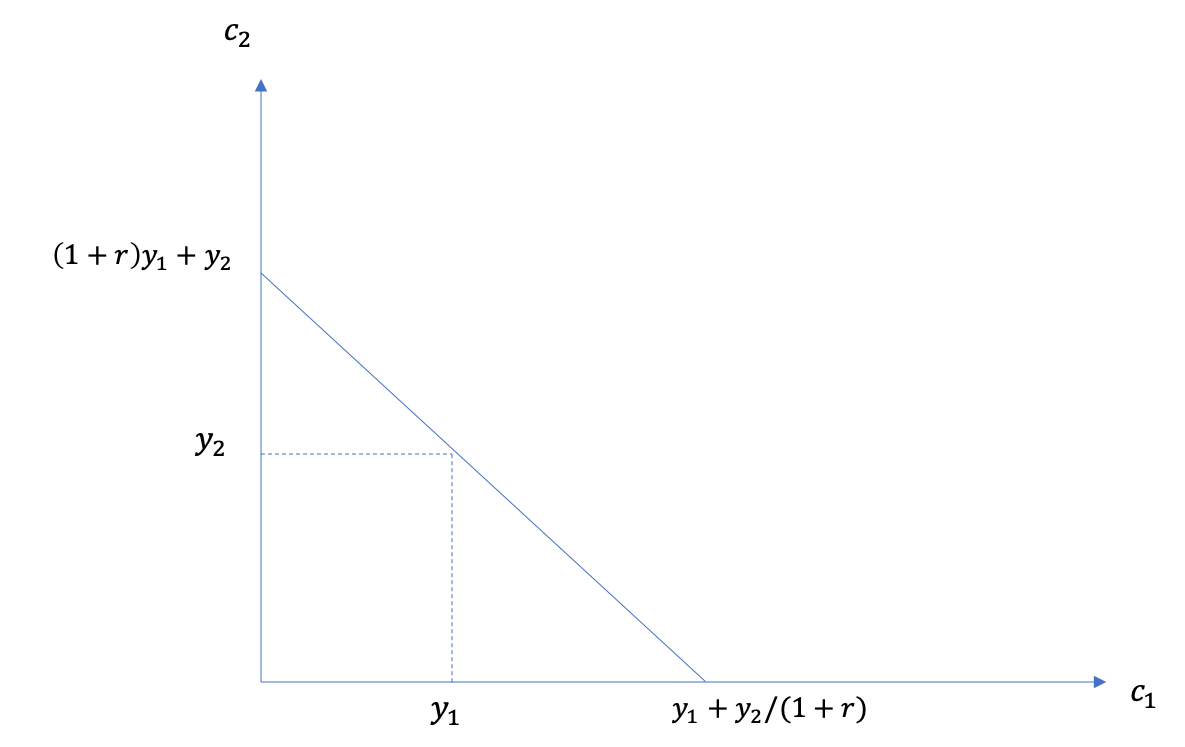
À faire
Testez vos intuitions sur EconGraph.org.
Exemple: Un régime de retraite à prestation déterminé force l’individu à épargner dans la première période et donne un revenu additionnel dans la deuxième.
Revenu en 2e période est \(Y_2 = \phi Y_1\) avec un taux de remplacement \(\phi \in [0,1]\).
Le revenu de première période est amputé d’une contribution \(\tau Y_1\).
La contrainte budgétaire est donc:
Le taux de contribution est choisi par l’actuaire \(\tau\) tel que:
où \(r_P\) est le taux de rendement implicite du régime de retraite. Si \(r_P = r\), la contrainte budgétaire ne change pas! Le plan de consommation ne change pas et donc l’épargne privée est réduite d’un même montant que la contribution (Effet d’éviction).
Écarts de taux emprunts vs. épargne
À faire
Exercice B: À quoi ressemble la contrainte si \(r_S<r_D\)?
À faire
Exercice C: Comment représenter une situation où l’agent ne peut emprunter?
Choix optimal
Maximisation
Le problème est (fixons \(W_0=0\) pour simplifier):
Deux approches:
Approche directe (substitution de la contrainte)
Lagrangien
Conditions d’optimalité
Le Lagrangien a 3 CPO:
Avec (1) et (2) on obtient :
Important
Le consommateur choisi son niveau de consommation tel que la valeur d’augmenter sa consommation de première période (TMS) est égal au coût d’opportunité de le faire en terme de consommation de deuxième période.
À faire
Testez vos intuitions sur EconGraph.org.
On peut réarranger et en fixant \(R=1+r\), on obtient l’équation de Euler:
Important
Le consommateur cherche à lisser l’utilité marginale dans le temps.
Visuellement
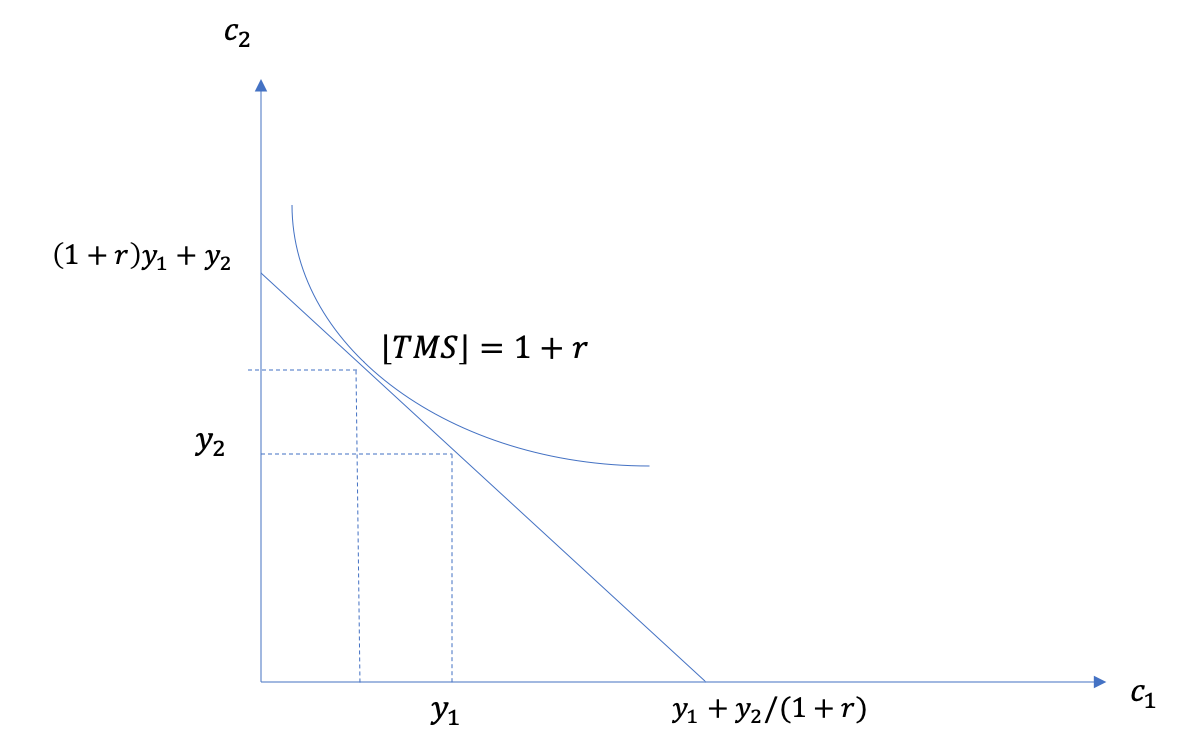
Cette théorie serviva de fondation pour la théorie du cycle de vie (the Life-Cycle Hypothesis), proposée par Franco Modigliani, qui permettra de comprendre les choix en fonction de l’âge d’un agent. L’équation de Euler dérivée ici-haut suggère qu’un individu aime lisser sa consommation sur le cycle de vie, et par conséquent, s’il fait face à des revenus élevés durant sa carrière et faibles plus tard, il épargnera quand il est jeune et consomme cette épargne quand il est plus vieux. Ceci servira de fondation pour l’étude de l’épargne, de l’assurance-vie, de l’immobilier et d’un tas d’autres décisions financières.
À faire
Exercice D: Trouvez le choix optimal de \(C_1\) et \(C_2\) si \(u(C)=\frac{C^{1-\sigma}}{1-\sigma}\) et avec une contrainte budgétaire classique.
Exemple: Épargne-t-on assez pour la retraite?
Une question très présente dans le débat public…

Le Conseiller, Globe and Mail, L’Actualité
On peut simuler des taux de remplacement effectif avec des modèles sophistiqués, mais difficiles de dire ce qui est assez ou non…
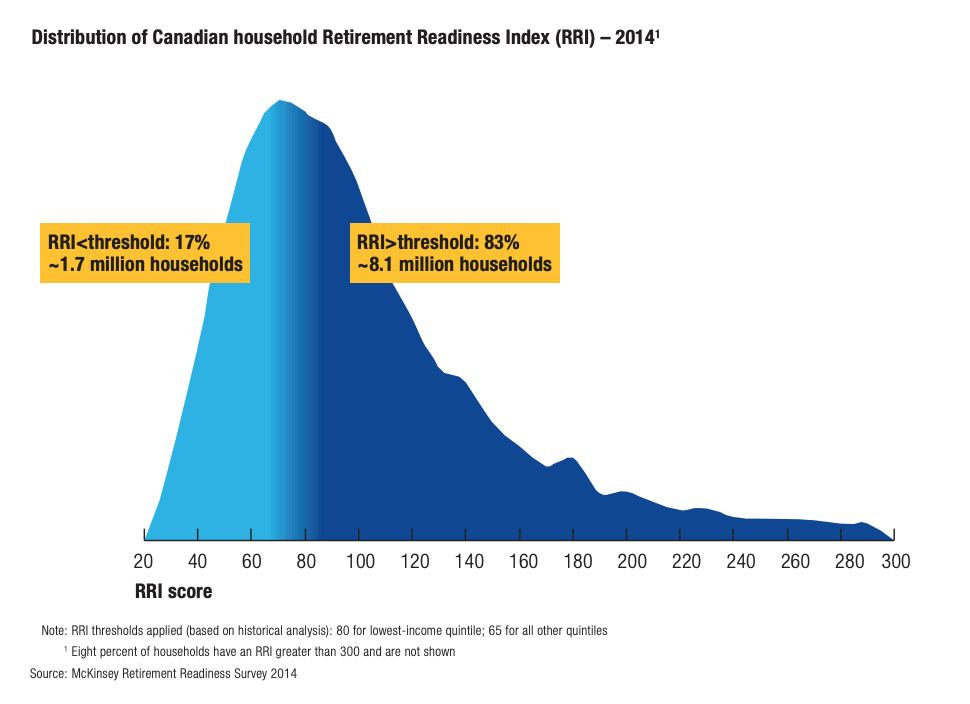
McKinsey (2015)
Pour des calculs plus récents, voir ce rapport de l’Institut Retraite et Épargne à HEC.
Épargne optimale
Qu’est-ce que la théorie nous dit sur l’épargne optimale?
À faire
Exercice E: Trouvez une expression pour le niveau optimal d’épargne en début de 2e période si \(u(C)=\frac{C^{1-\sigma}}{1-\sigma}\) et la contrainte est donnée par:
Des calculs plus sophistiqués peuvent être fait pour comparer l’épargne accumulée à la retraite à l’épargne optimale selon un modèle:
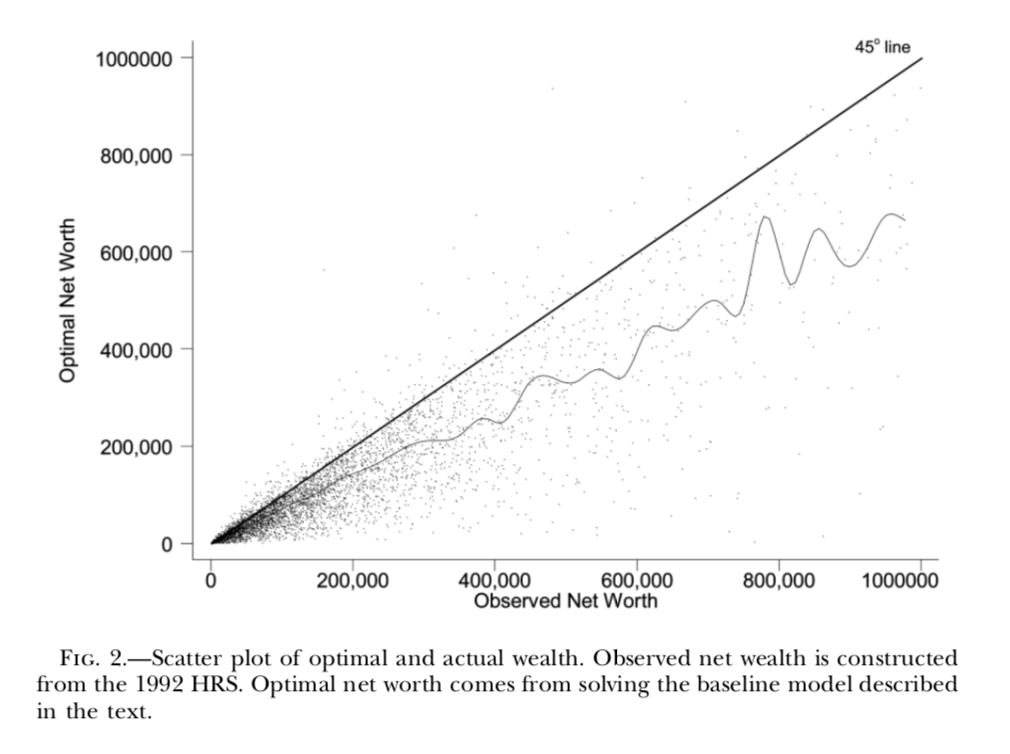
Les conclusions sont parfois surprenantes comparativement à ce qu’on observe dans les médias. Une grande majorité semble épargner assez. Certains épargnent trop, ce qui sous-optimal.
Microéconomie en action: Épargne-retraite
Regardez cet entretien avec Bernard Morency, professeur associé à HEC Montreal expert de renommée mondiale sur les retraites.
Biais pour le présent
Comme nous l’avons vu, les gens peuvent être très impatients. Mais leur préférence peut tout de même respecter les principes de l’utilité escomptée. Cependant, il existe plusieurs violations de l’utilité escomptée. Nous nous concentrons ici sur le biais pour le présent.
Exemple: Choisir un film
Vous devez choisir un film à regarder aujourd’hui et un la semaine prochaine:
Supposons que Mommy a un bénéfice immédiat de 4 et un bénéfice futur de 4, mais que Les Boys a un bénéfice immédiat de 7 (aucun bénéfice futur).
À faire
Exercice F: Quel est l’utilité escomptée si vous choisissez aujourd’hui et \(\delta=1\). Que se passe-t-il si vous choisissez plutôt pour la semaine prochaine (et la suivante, donc vous ne regardez rien cette semaine)?
L’évidence empirique montre que les gens préfèrent les Boys si le choix se fait aujourd’hui, mais Mommy si le choix est fait pour la semaine prochaine. L’utilité escomptée ne permet pas d’expliquer que le choix dépend de l’horizon. Cet exemple est un parmi d’autres d’incohérence intertemporelle.
Biais pour le présent
Laibson (1997) propose une modification assez simple aux préférences escomptées, soit l’introduction d’une fonction d’escompte quasi-hyperbolique:
Le paramètre \(\beta\) agit comme paramètre de biais pour le présent (facteur d’escompte à court terme) alors que \(\delta\) contrôle l’impatience à long terme. Ces préférences dépendent maintenant de l’horizon…
À faire
Exercice G: Quel est le TMS entre les consommations \(C_1\) et \(C_2\)? Et \(C_2\) vs. \(C_3\)? Comparez avec l’espérance d’utilité.
En utilisant l’exemple des deux films, supposons maintenant \(\beta=0.5\).
À faire
Exercice H: Refaire l’exercice F. Quel film choisissez-vous pour aujourd’hui et pour la semaine prochaine si vous avez des préférences quasi-hyperboliques? Que ferez vous une fois la semaine prochaine?
Les préférence quasi-hyperboliques capturent bien ces renversements de choix.
Exemple: Qui s’abonne au Gym?
Dans un article, Della Vigna et Malmendier (2006) étudie le choix de prendre un abonnement au Gym plutôt que d’acheter des passes individuelles. Une passe d’une visite coûte 10$. Le coût par visite des gens qui s’abonne est beaucoup plus élevé que 10$. Pourquoi les gens achètent-ils un abonnement? Sont-ils naïfs par rapport au fait qu’ils ont des préférences quasi-hyperboliques?
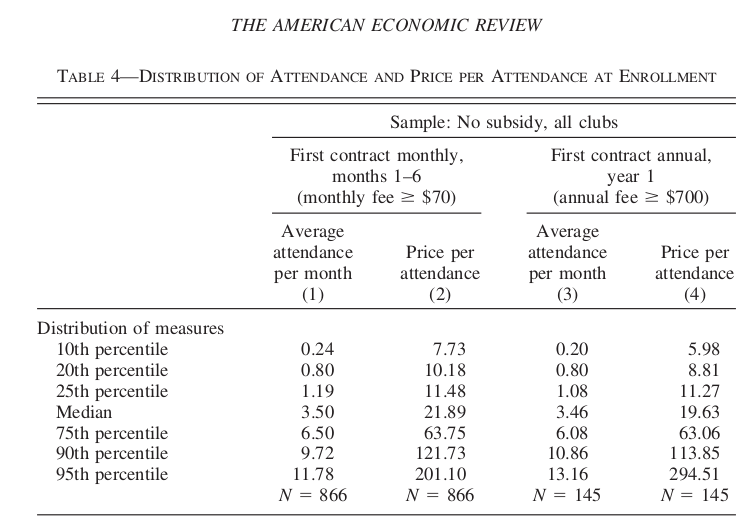
Il y a évidence que certains sous-estiment leur degré de biais pour le présent. Ils sont naïfs par rapport à leur problème de biais pour le présent.
Exemple: Comment aider les gens à épargner?
Épargner est similaire à aller au Gym: coûteux dans le court-terme (sacrifice de consommation), bénéfique à long terme (consommation future).
Pour aider les gens avec ces biais, on pourrait décider de changer l’option de défaut: opt-in vs. opt-out. Au lieu de devoir décider d’épargner (défaut = n’épargne pas), on peut par défaut forcer les gens à épargner et ils peuvent arrêter s’ils le veulent (défaut = épargne) … Ce petit changement a de gros impacts.
Shea et Madrian (2001, QJE) montrent que l’épargne, à court terme pour les entreprises qui changent le défaut, augmente.
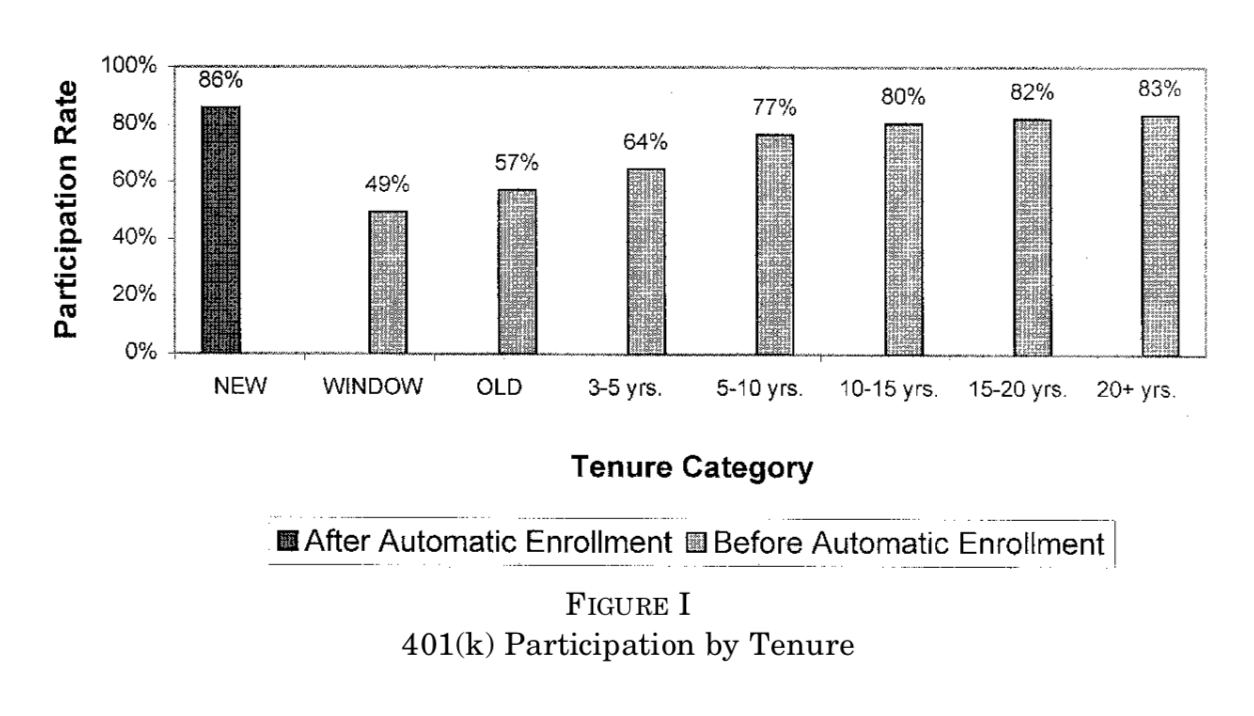
Moins évident à long terme…
Engagement
Les gens aux prises avec un problème de la sorte pourraient vouloir, rationnellement, qu’on limite leur choix. Par exemple, en ne leur permettant pas de succomber à la temptation à court terme dans leur propre intérêt. David Laibson de Harvard, et plusieurs autres étudient des mécanismes de la sorte, appliquées à la santé et l’épargne par exemple. Il semblerait qu’il y a une demande pour ces mécanismes (demand for commitment).
Exemple Python Intertemporel
Voir cet exemple Python qui permet d’approfondir ces concepts.