Effets Prix et Revenu
La question visant à évaluer comment les consommateurs réagissent à des changements de prix et de revenu est au centre de l’étude des comportements économiques. En particulier parce que les prix et les revenus sont affectés par les politiques publiques. Par exemple, on voudrait pouvoir répondre à une question comme:
Est-ce qu’une taxe sur l’essence réduit la consommation d’essence et encourage le transport en commun?
Pour le savoir, on doit étudier empiriquement comment la demande d’essence et de transport en commun réagit à une taxe sur l’essence. On veut peut-être aussi comprendre si cette taxe sera régressive (si elle aura un effet important sur le pouvoir d’achat des moins nantis). Si on veut les compenser, il faudra connaître les effets prix et revenus.

Les gilets jaunes en France ont manifesté entre autres parce que de nouvelles taxes sur le carburant réduisaient leur pouvoir d’achat.
Les élasticités prix et revenu peuvent être estimées sans théorie. Mais comment utiliser ces informations pour répondre aux questions plus normatives?
La théorie sur le choix du consommateur nous fournira un bon nombre de pistes.
Demande et Préférences
Formalisons cet exemple:
Essence (\(X\)) et Transport en commun (\(Y\))
Utilité \(u(X,Y)\)
Contrainte budgétaire: \(p_X Y+ p_Y Y \leq I\)
Les fonctions de demande \((X^*, Y^*)\) sont telles que
À l’optimum, le budget est respecté et le consommateur est indifférent entre réduire \(X\) pour augmenter \(Y\) (et vice versa).
Il y a deux équations, deux variables: la solution pour \(X^*\) et \(Y^*\) en fonction de \((p_X,p_Y,I)\) donne les demandes marshalliennnes.
Exemple
Pour les préférences représentées par \(u(X,Y) = \log X + 2\log Y\),
On utilise \(p_X X + p_Y Y = I\) ce qui permet d’obtenir
Comment \(X^*\) et \(Y^*\) varient en fonction de \(I\) et des prix?
Effets revenu
Débutons avec les changements de revenu.
Courbe d’Engel
Le consommateur demande \(X(p_X,p_Y,I)\) et \(Y(p_X,p_Y,I)\).
La courbe d’Engel pour \(X\): Comment \(X^*\) change quand \(I\) change?
Proportion du budget dédié à \(X\): \(s_X = \frac{p_X X}{I}\)
Bien normal
Note
Un bien est normal si et seulement si la demande de ce bien augmente avec le revenu (prix constant)
Bien inférieur
Note
Un bien est inférieur si sa demande diminue quand le revenu augmente (à prix constant)
L’essence est-elle un bien inférieur ou normal? Qui consomme l’essence? Une étude de James Porterba suggère que même si on pourrait croire que l’essence est un bien inférieur, ceci dépend si on mesure en proportion du revenu ou des dépenses (Poterba, 1991)? La raison: la prise en compte de l’épargne utilisée pour consommer des biens.

Pour quantifier les effets revenus, on voudra utiliser une élasticité-revenu de la forme:
Comment calculer l’élasticité? Si \(X^* = \frac{I}{3p_X}\), alors on a
Des demandes marhalliennes provenant d’une fonction Cobb-Douglas ont toujours une élasticité revenu de 1. Pourquoi? Parce que la part d’un bien dans le budget est fixe, \(s_X = \frac{p_X X^*(p_X,p_Y,I)}{I} = \alpha\) si \(u(X,Y) = X^{\alpha} Y^{1-\alpha}\). Donc si le revenu augmente de 10%, la demande augmente de 10% pour que la part de X dans le budget reste inchangée.
En pratique, il n’est pas facile d’estimer ces élasticités-revenu en s’assurant que le changement de revenu est exogène. En effet, on voudra contrôler pour les différences de préférences selon le revenu.
Quel type d’événement pourrait-on exploiter?
Si on suppose l’élasticité constante, considérons le modèle économétrique suivant:
où \(i\) dénote une paire d’observations (donnée sur des individus) et \(\epsilon_{i}\) un terme d’erreur indépendant du revenu. Alors, on a que
mais aussi que
Donc \(\beta\) est égal à \(\eta_{X,I}\). Une élasticité revenu peut être estimée par la pente dans une régression linéaire du log de la quantité du bien (ou des dépenses si le prix est fixe) sur le log du revenu. Une estimation de l’élasticité est donc
À faire
Regardez cet exemple de EconGraph.org
Effets Prix
Comment les demandes \(X^*\) et \(Y^*\) changent si \(p_Y\) et \(I\) restent constants, mais que \(p_X\) change?
Pour décrire les changements de demande, on utilise l’élasticité:
Elle est invariante aux unités monétaires. Qu’en est-il pour la fonction d’utilité Cobb-Douglas?
L’élasticité prix d’une fonction Cobb-Douglas est égale à 1 (en valeur absolue). Encore une fois, ceci découle de la propriété sur les parts fixes. Si le prix augmente de 10% et que le revenu ne change pas, la seule façon de garder la part fixe est de diminuer la quantité de 10%, ce qui donne une élasticité de -1.
Encore une fois, un enjeu important est d’estimer cette élasticité dans un contexte où le changement de prix qui est exogène. Heureusement, il y a les taxes qui changent parfois pour des raisons indépendantes de la demande… Sinon, des chocs d’offre (manipulation du prix d’un cartel, désastre naturel).
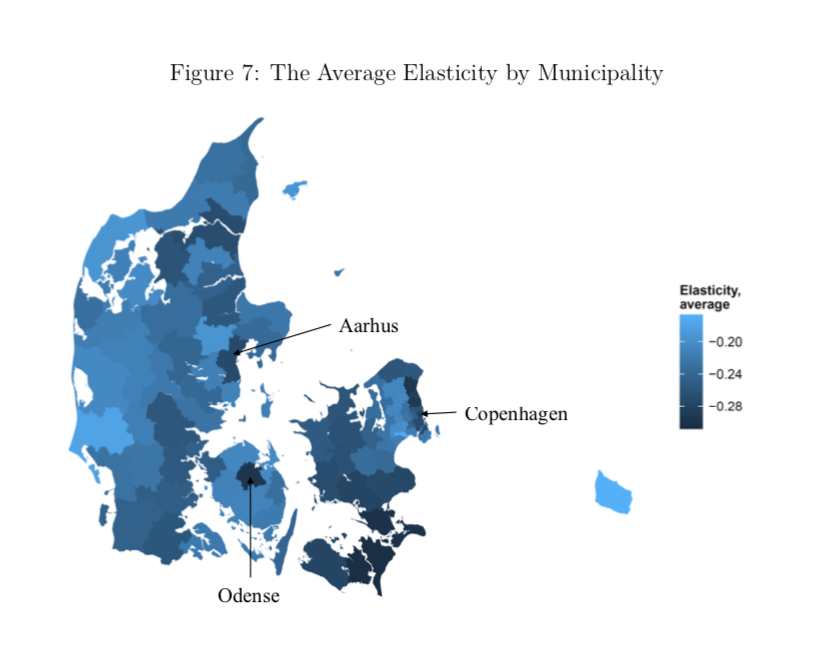
Au Danemark, une étude montre que l’élasticité varie considérablement à travers le pays et en particulier dépendant de la distance qu’ont à faire les gens chaque jour.
Au États-Unis, une autre analyse montre qu’il faut faire la distinction entre l’effet d’un changement de prix et une taxe. L’effet d’une taxe est plus important? Pourquoi? Une taxe est p-e plus visible.
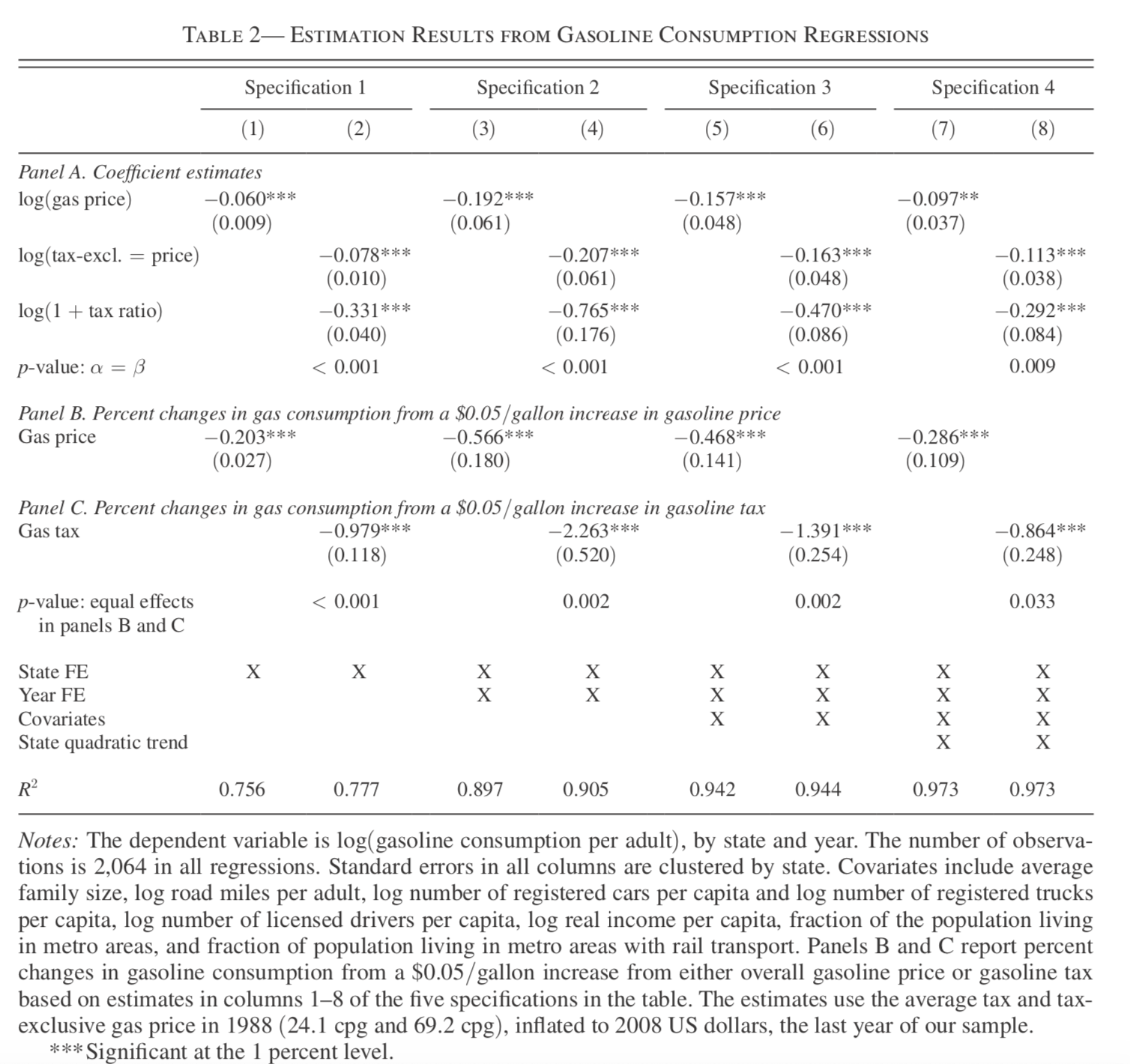
Quelles implications pour les revenus de taxes? L’élasticité est un paramètre clé. Quand l’élasticité est supérieure à 1 (en value absolue), une hausse de la taxe diminue les revenus du gouvernement.
Une hausse de prix (ou taxe) a l’effet direct de réduire le bien-être du consommateur. On pourrait vouloir compenser certains ménages parce que la taxe poursuit un bon objectif économique (e.g. climat, redistribution). Afin de calculer la compensation possible suite à une taxe, il faut décomposer le changement de demande pour l’essence quand le prix \(p_X\) augmente. Il y a deux forces:
Le transport en commun est plus abordable que l’automobile (essence): le consommateur voudra substituer vers le transport en commun. C’est un effet substitution qui provient du signal de prix.
\[\frac{u'_X(X,Y)}{u'_Y(X,Y)} = \frac{p_X}{p_Y}\]Besoin de plus de revenus pour acheter le même panier de référence (réduction pouvoir d’achat): effet revenu.
La compensation est fonction de ces deux effets. Notre objectif comme analyste est d’identifier les effets prix et revenu afin de mieux .évaluer les impacts sur le bien-être et sur les comportements d’une compensation.
Effets revenu et substitution en action
Voir cette entrevue réalisée avec Justin Caron, professeur agrégé à HEC Montréal, sur les effets d’une taxe carbonne.
Demande compensée
La demande compensée est un passage obligé. Elle permettra de séparer ces effets.
Contexte
Prix de référence \((p_X,p_Y)\), revenu de référence \(I\),
Nouveau prix \((\hat p_X,p_Y)\), revenu ne change pas.
Demande de référence \(X(p_X,p_Y,I)\), utilité indirecte de référence \(v(p_X,p_Y,I)\)
Nouvelle demande \(X(\hat p_X, p_Y, I)\), nouvelle utilité indirecte \(v(\hat p_X,p_Y,I)\).
Le concept de revenu compensé: revenu \(I^{cmp}\) tel qu’on peut préserver le niveau d’utilité de référence aux nouveaux prix.
\[v(p_X,p_Y, I) = v(\hat p_X, p_Y, I^{cmp})\]
La demande compensée (ou hicksienne) est donnée par la demande marshallienne où l’on remplace le revenu par le revenu compensé \(X^{cmp}= X(\hat p_X, p_Y, I^{cmp})\).
Important
Le revenu compensé pour une hausse de prix est toujours plus élevé que le revenu de référence. La différence est la compensation requise. Si la hausse de prix est une nouvelle taxe, cette compensation est la compensation requise pour maintenir le bien-être du consommateur constant tout en ayant modifié les comportements.
À faire
Exemple de variation compensatoire EconGraph.org.
À faire
Demande marshallienne et hicksienne en action EconGraph.org.
Voir aussi
Il existe un problème dual du consommateur ou on trouve la demande compensée par le biais de la minimisation des dépenses étant donné un niveau d’utilité à atteindre. Nous ne traitons pas de ce problème dual dans le cours.
Loi de la demande compensée Si \(\hat p_X > p_X\), alors \(X^{cmp}(\hat p_X,p_Y,I)<X(p_X,p_Y,I)\). La demande compensée \(X\) est décroissante dans le prix \(p_X\).
À faire
Exercice A: Calculez le revenu et la demande compensée pour \(X\) si \(U(X,Y) = XY\) et \(p_XX+p_YY \le I\) pour un changement de prix \(\hat p_X > p_X\).
On peut calculer le revenu compensé pour un problème plus général numériquement. On débute par reprendre les fonctions de demande et l’utilité indirecte.
def x_d(p_x,p_y,I,alpha):
return alpha*I/p_x
def y_d(p_x,p_y,I,alpha):
return (1-alpha)*I/p_y
def v(p_x,p_y,I,alpha):
xstar = x_d(p_x,p_y,I,alpha)
ystar = y_d(p_x,p_y,I,alpha)
return u(xstar,ystar,alpha)
Ensuite, on a besoin de l’égalité suivante:
Donc, nous cherchons \(I^{cmp}\) qui fait en suite que la différence entre le côté droit et gauche de l’équation est zéro. On peut écrire cette fonction (l’argument est la compensation \(\Delta I^{cmp} = I^{cmp} - I\)):
def slack(cmp,p_x,dp_x,p_y,I,alpha):
return v(p_x,p_y,I,alpha) - v(p_x+dp_x,p_y,I+cmp,alpha)
Si on évalue à zéro, on aura quelque chose de positif (le consommateur n’aime pas une hausse de prix), et si cmp est très grand, on aura quelque chose de négatif (on compense trop). L’objectif est donc de trouver cmp tel que la fonction slack() est zéro. L’algoritme bisect permet de faire ce travail,
from scipy.optimize import bisect
cmp = bisect(slack,0,I,args=(p_x,dp_x,p_y,I,alpha))
La fonction retourne la compensation nécessaire avec un changement de prix de dp_x. Le notebook ici-bas vous permettra de vous familiariser avec cette technique.
Précisons maintenant davantage les effets substitutions et revenu.
Effet substitution
Changement de demande causé par un changement de prix relatif, en gardant l’utilité constante.
Effet substitution \(=\) Demande compensée - Demande de référence
\[\Delta X^{{cmp}} = X(\hat p_X,p_Y,I^{cmp}) - X(p_X,p_Y,I)\]
Effet revenu
Changement de la demande causé par un changement du pouvoir d’achat, en gardant les prix constants.
Effet revenu \(=\) Nouvelle demande - demande compensée
On peut approximer le revenu compensé pour un petit changement de prix paramétrisé
\(\hat p_X = p_X + \Delta p_X\).
Pour nettoyer la notation et y voir clair, dénotons
\(X^* = X(p_X,p_X,I)\), \(Y^* = Y(p_X,p_Y,I)\)
Définissons ensuite \(I^{cmp}= I + \Delta I^{cmp}\), \(X^{cmp}= X^* + \Delta X^{cmp}\) et \(Y^{cmp}= Y^* + \Delta Y^{cmp}\).
Alors,
Pourquoi \(p_X\Delta X^{{cmp}} + p_Y \Delta Y^{{cmp}} = 0\)?
\((X^*,Y^*)\) et \((X^{cmp},Y^{cmp})\) sont sur la même courbe d’indifférence, ce qui implique,
\[\frac{\Delta Y^{cmp}}{\Delta X^{cmp}} = TMS_{X\to Y}\]
\((X^*,Y^*)\) est optimal aux prix \(p_X, p_Y\), ce qui implique que \(TMS_{X\to Y} = -\frac{p_X}{p_Y}\).
Alors, \(p_X \Delta X^{cmp}+ p_Y \Delta Y^{cmp}= 0\).
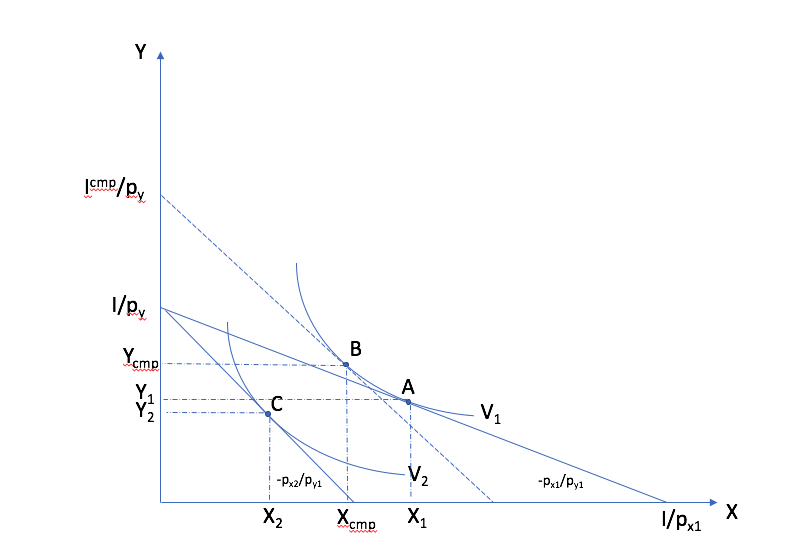
Dans l’espace \((X,Y)\), nous considérons une augmentation de prix du bien \(X\), L’indice 1 réfère à la situation de référence et l’indice 2 à la situation après le changement de prix. Le consommateur est au point A dans la situation de référence. Avec le changement de prix, la contrainte budgétaire a une pente plus forte. Après le changement de prix, le consommateur est au point C. Pour décomposer le changement de prix, on compense le consommateur aux nouveaux prix. Il choisit alors le point B, avec la même utilité que dans la situation de référence. Le passage du point A au point B est l’effet substitution. L’effet revenu se mesure du point B au point C. La somme des deux donne l’effet total.
À faire
Exercice B: Voir si cette approximation est bonne pour \(U(X,Y) = XY\) avec prix et revenu de référence \((p_X,p_Y,I) = (1,1,100)\) et \(\Delta p_X = 1\). Trouvez les effets substitution (prix) et revenu.
Équation de Slutsky
L’équation de Slutsky permet de relier l’effet prix total, l’effet substitution (compensé ou hicksien) et l’effet revenu. Le premier et le dernier sont observables, le 2e ne l’est pas et est nécessaire pour calculer une compensation.
Pour garder la notation simple, considérons
On obtient
Puisque
alors,
En termes d’élasticités, on multiplie à gauche et droite par \(\frac{p_X}{\Delta p_X X^*}\) et on multiplie le dernier terme par \(I/I\). On obtient,
Finalement, on note que \(\frac{\partial X}{\partial I} = \eta_{X,I}\frac{X^*}{I}\). En remplacant et en dénotant la part du revenu consacrée à \(X\) comme étant \(s_X = \frac{p_X X^*}{I}\), l’équation de Slutsky est donc
Quand le bien est normal, l’effet compensé est toujours plus faible que l’effet total. Les deux forces, substitution et revenu, vont dans le même sens et une augmentation de prix diminue la demande et l’utilité de l’agent. Quand on compense l’agent, on n’a que l’effet substitution. Un corrolaire est donc que pour un bien normal, le versement d’une compensation diminue l’effet du changement de prix (ou taxe) sur les comportements.
Plus la part d’un bien est importante dans le revenu, plus la compensation versée doit être élevée (l’effet revenu est plus fort).
À faire
Exercice C: Pour les préférences Cobb-Douglas \(u(X,Y) = X^\alpha Y^{1-\alpha}\), calculez l’élasticité prix compensé à l’aide de l’équation de Slutsky.
Effets prix croisés
D’abord, on peut inférer la nature des biens par les fonctions de demande. Les biens \(X\) et \(Y\) sont:
Substituts: si l’effet prix croisé \(\frac{\partial X^{cmp}}{\partial p_Y} >0\)
Compléments: si l’effet prix croisé \(\frac{\partial X^{cmp}}{\partial p_Y} <0\)
Qu’en est-il pour le transport en commun et les taxes sur l’essence? Cette élasticité est-elle importante pour la politique publique? Comment pourriez-vous l’estimer?
Propriétés des fonctions de demandes
Les fonctions de demandes ont certaines propriétés importantes qui découlent des axiomes sur les préférences et la maximisation de l’utilité:
Homogénéité de degré zéro (absence d’illusion monétaire)
\[X(\lambda p_X,\lambda p_Y,\lambda I) = X(p_X,p_Y,I)\]Symmétrie:
\[\frac{\partial X^{cmp}}{\partial p_Y} =\frac{\partial Y^{cmp}}{\partial p_X}\]Additivité:
\[p_X \frac{\partial X(p_X,p_Y,I)}{\partial I} + p_Y \frac{\partial Y(p_X,p_Y,I)}{\partial I} = 1\]Negativité (loi de la demande compensée):
\[\frac{\partial X^{cmp}}{\partial p_X}<0,\frac{\partial Y^{cmp}}{\partial p_Y}<0\]
Indices de prix et de coût de la vie
Pour mesurer un changement du coût de la vie (pouvoir d’achat), on utilise des indices de prix à la consommation. Un indice souvent utilisé est l’indice de Laspeyres:
Ainsi \(X\) et \(Y\), consommé dans la situation de référence, sont aussi utilisées après le changement de prix. L’indice des prix à la consommation garde les quantités (part des dépenses) fixes dans le court terme (les changent, mais pas très fréquemment). Plusieurs prestations gouvernementales sont indexées annuellement de la sorte afin de maintenir le pouvoir d’achat (pensions, crédit d’impôt, etc). Mais est-ce un bon indice pour mesurer une variation du coût de la vie?
La théorie qu’on vient de voir indique qu’il faut tenir compte des réactions comportementales. Si le prix d’un bien augmente, il y aura substitution. Pour bien mesurer la consommation, on revient à la théorie:
Après une augmentation de prix du bien \(X\), la compensation nécessaire pour garder le bien-être constant est:
\[\pi_I = \frac{I^{cmp}}{I}\]
Tout dépendant des préférences, il se peut que l’indice de prix hicksien donne une réponse différente de l’indice de Laysperes. En particulier, si la part d’un bien décroit si son prix augmente, l’indice Hicksien pourrait donner une augmentation du coût de la vie plus faible qu’un indice de type Laysperes. C’est ce qu’on appelle un biais de substitution.
Avec la pandémie et le confinement, la consommation d’essence a chuté. Le prix de l’essence a aussi chuté (pour pleins de raisons, incluant une décision des cartels). Est-ce qu’un indice de Laysperes donne un bon reflet du changement du pouvoir d’achat dans un tel contexte? Cet article fait le calcul pour les États-Unis et montre que l’inflation est sous-estimée considérablement.
Les entreprises et l’analyse de la demande
Pourquoi une entreprise devrait-elle étudier les propriétés de la demande pour ses biens? Elle peut potentiellement augmenter ses revenus en:
fixant un prix qui maximise ses revenus si elle a un pouvoir de marché
discriminant par les prix (segmentation)
L’analyse économétrique peut être utilisée à partir des données de l’entreprise, ou du marché (scanner data?) pour estimer différentes élasticités.
Exemple Effet prix et revenu
Voir ce notebook pour un exemple qui utilise Python pour calculez la compensation et trouvez les effets prix et revenu avec fonction d’utilité CES (Constant Elasticity of Substitution)